物理のノート

電磁気回路の基礎と応用

LRC回路とインピーダンス整合

LRC直列回路の回路方程式と制御特性

直流の電圧源$V_i(t)$を直列配置したLRC回路に接続する. その際, コンデンサーCに蓄積される電気量$q(t)$を考える. \begin{equation} L\frac{d^2 q}{dt^2}+R\frac{dq}{dt}+\frac{1}{C}q=V_i(t) \end{equation} 以下の図は, LTSpiceで描画した一例である.

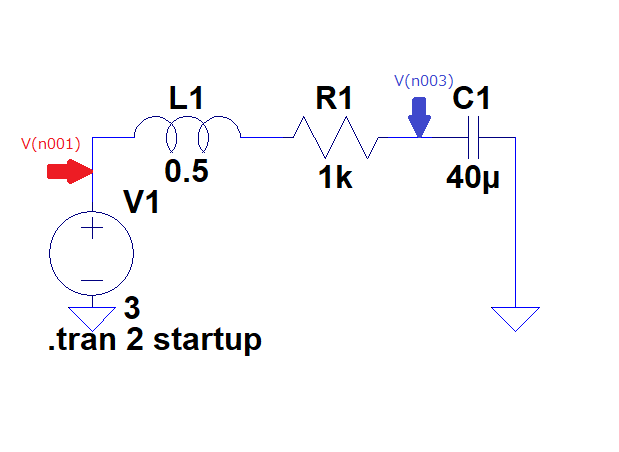
書物では"RLC回路"と表記されることが多いが, 回路方程式に現れるL, R, Cの順番から個人的には"LRC回路"の方が理解しやすく, 本稿ではそう表記している.

さて, 式(1)の両辺を時間t（$0$から$t$まで）で積分する. \begin{equation} L\frac{dq}{dt}+RI+\frac{1}{C}\int_0^t qdt=\int_0^t V_i dt=f_i(t) \end{equation} 電流$I=\int_0^t dq $

式(2)左辺の第1項をD（Differencial：微分）動作, 第2項をP（Proportional：比例）動作, 第3項をI（Integral：積分）動作と称する.

微分動作（D動作）は, LRC回路において位相を遅らせる遅相（インダクタンス）を表す. 一方, 積分動作（I動作）は進相（キャパシタンス）を意味す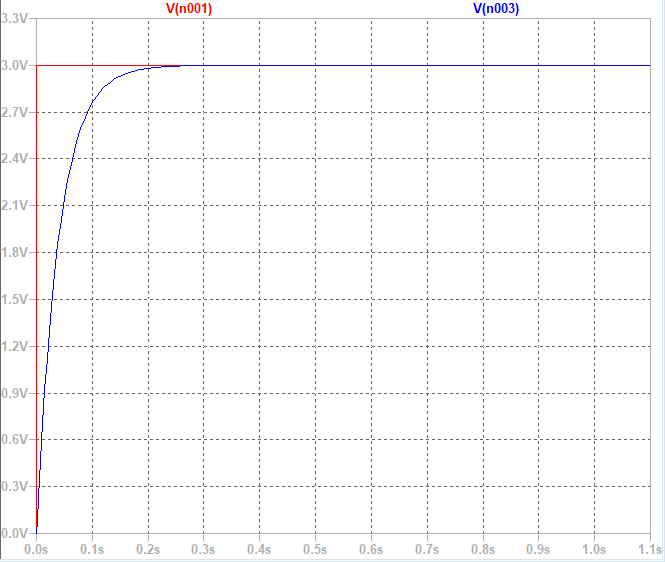る.

P, I, D動作が結合されたPID動作により, 出力電圧が入力電圧（この例の回路では$3V$）に近づく. 時間とともに応答が安定化していくステップ応答のイメージを表している.

個人的には, "PID動作"というよりは, L, R, Cの順番に足並みを揃えて, "DPI動作"と呼んだ方がしっくりくる.

index.htmlに戻る