物理のノート
公式類>フーリエ解析
方形パルスのフーリエ変換
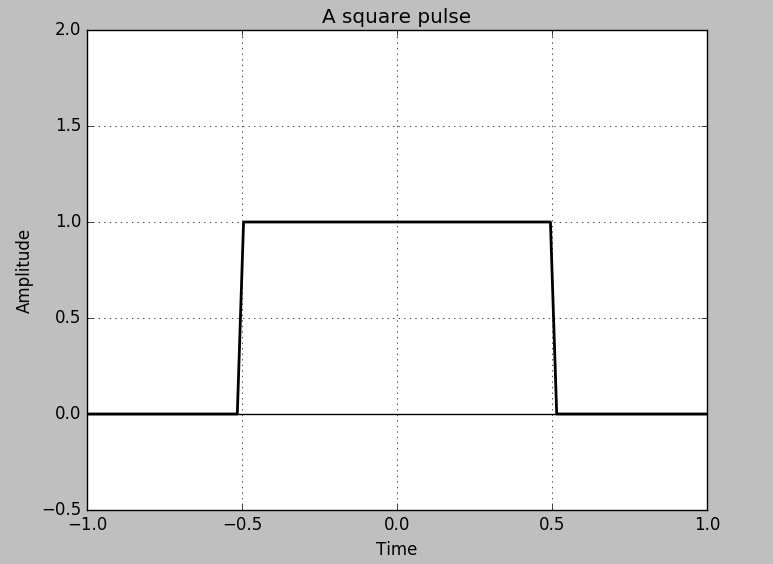
次のような方形パルスをフーリエ変換する（図は$d=1$）.
\begin{equation}
f(x)=\binom{1(\lvert x \rvert \lt \frac{d}{2})}{0(\lvert x \rvert \gt \frac{d}{2})}
\end{equation}
$f(x)=1$$(-\frac{d}{2} \lt x \lt \frac{d}{2} )$として, フーリエ変換の定義より,
\begin{equation}
F(\omega)=\int_{-\infty}^{\infty} f(x) e^{-i \omega x}dx\\
=\int_{-\frac{d}{2}}^{\frac{d}{2}}e^{-i \omega x}dx\\
=-\frac{1}{i\omega}\left[e^{-i \omega x}\right]_{-\frac{d}{2}}^{\frac{d}{2}} \\
=-\frac{1}{i\omega}(e^{-i \frac{\omega d}{2}}-e^{i \frac{\omega d}{2}})\\
=\frac{2}{\omega}\sin \left(\frac{\omega d}{2}\right)\\
=d\frac{\sin\frac{\omega d}{2}}{\frac{\omega d}{2}}\\
=d\frac{\sin x}{x}.
\end{equation}
$x=\frac{\omega d}{2}$と置き換える.
(2)式より, フーリエ変換後の関数をグラフ上にプロットする.
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(8,6), dpi=100)
ax = fig.add_subplot(111)
d = 1
x = np.linspace(-20,20,100)
y = d * ((np.sin(x))/x)
plt.plot(x,y, linewidth=2, color='blue')
plt.ylim(-4, 10)
ax.grid(True)
plt.axhline(y=0, color='k')
plt.show()
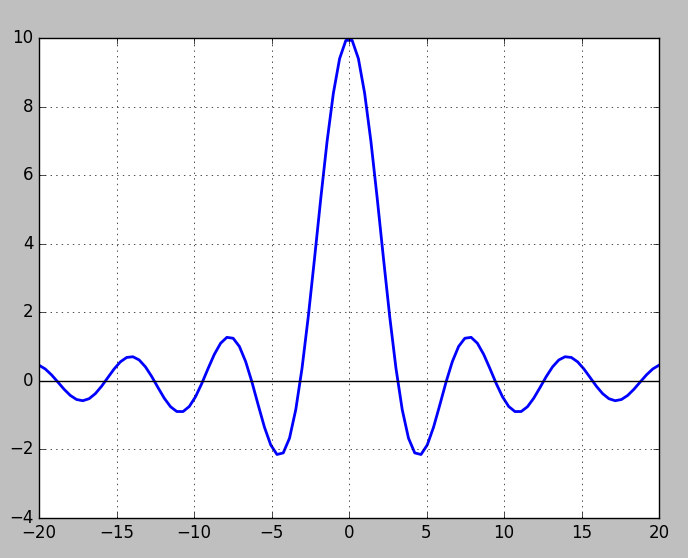
$d=10$の場合は,下図のようにプロットされる.
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(8,6), dpi=100)
ax = fig.add_subplot(111)
d = 10
x = np.linspace(-20,20,100)
y = d * ((np.sin(x))/x)
plt.plot(x,y, linewidth=2, color='blue')
ax.grid(True)
plt.axhline(y=0, color='k')
plt.show()
方形パルスの幅$d$が大きい（広い）ほど,そのフーリエ変換後のグラフの最大振幅が大きく（高く）なることが伺える.
index.htmlに戻る