物理のノート
公式類>フーリエ解析
方形波(矩形波)のフーリエ級数
奇関数の場合
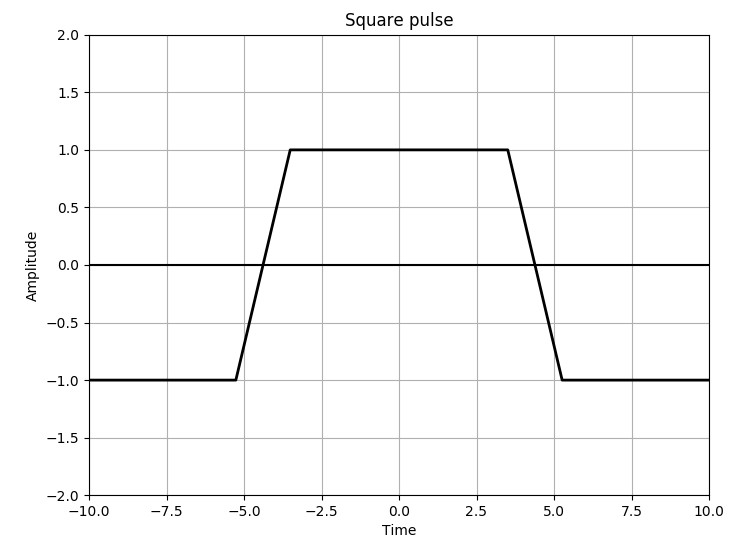
デジタル信号などで見られる方形波(矩形波)は次のような形をしている.

# -*- coding: utf-8 -*-
from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(8,6), dpi=100)
ax = fig.add_subplot(111)
x = np.linspace(-100, 100, 115, endpoint=True)
y = 1 * signal.square(np.pi * (x+1))
plt.plot(x, y,linewidth=2, color='k')
plt.ylim(-2, 2)
plt.xlim(-10, 10)
plt.axhline(y=0, color='k')
plt.title('Square pulse')
plt.xlabel('Time')
plt.ylabel('Amplitude')
ax.grid(True)
plt.show()
上記のグラフでは台形になっているが,これを$t=0$で$f(t)=-1$および$1$を非連続に跳んでいる, とする(凹凸のように).
この方形波を表す関数をフーリエ級数展開する.
フーリエ級数の公式より,時間$t$の関数$f(t)$のフーリエ級数展開は,
\begin{equation}
f(t)=\frac{a_0}{2}+a_1\cos \omega t+a_2\cos 2\omega t+a_3\cos 3\omega t+ \dots +a_n\cos n\omega t \\
+\dots +b_1\sin \omega t+b_2\sin 2\omega t +b_3\sin 3\omega t+\dots +b_n\sin n\omega t+ \dots \\
= \frac{a_0}{2}+ \sum_{n=1}^\infty (a_n\cos n\omega t +b_n\sin n\omega t)
\end{equation}
と示されるが, この方形波は奇関数($f(t)=-f(-t)$)であるから, $\cos n\omega x$の項は消え,$\sin n\omega x$の項のみが残る(奇関数の場合と同様に, $ a_0=\frac{1}{\pi} \int_{0}^{2\pi} f(t)dt$も消える).すなわち, フーリエ係数$b_n$が残る($ a_0=\frac{1}{\pi} \int_{0}^{2\pi} f(t)dt$も消える).
$f(t)=\pm 1$として計算する.
フーリエ係数$a_0$は,
\begin{equation}
a_0=\frac{1}{\pi} \int_{0}^{2\pi} f(t)dt\\
=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)dt\\
=\frac{2}{T} \left\lbrace \int_{-\frac{T}{2}}^{0} -t dt + \int_{0}^{\frac{T}{2}} t dt \right\rbrace \\
=\frac{2}{T} \lbrace-[0-(-\frac{T}{2})] + [(\frac{T}{2})-0] \rbrace \\
=0.
\end{equation}
フーリエ係数$b_0$は,
\begin{equation}
b_n=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)\sin n\omega t dt \qquad (n=1,2,3 \dots )\\
=\frac{2}{T}\left\lbrace \int_{-\frac{T}{2}}^{0} -\sin n\omega t dt + \int_{0}^{\frac{T}{2}} \sin n\omega t dt\right\rbrace\\
=\frac{2}{T}\left\lbrace \left[\frac{1}{n\omega} \cos n\omega t \right]_{-\frac{T}{2}}^{0} + \left[ \frac{-1}{n\omega}\cos n\omega t\right]_{0}^{\frac{T}{2}} \right\rbrace\\
=\frac{2}{n\omega T}\left\lbrace [1-\cos (-n\pi)]- [ \cos n\pi -1] \right\rbrace\\
=\frac{2}{n\pi}(1-\cos n\pi)\\
=\frac{2}{n\pi}\lbrace 1-(-1)^n \rbrace .
\end{equation}
ここで,
\[
\cos n \pi=(-1)^n
\]
である.また
\[
\omega T=2\pi f T=2\pi
\]
である.
ゆえに,
\begin{equation}
b_n = \left\lbrace
\begin{array}{cc}
0 \qquad\text{nが偶数のとき} \\
\frac{4}{n\pi} \qquad\text{nが奇数のとき}
\end{array}
\right\rbrace
\end{equation}
これより,
\begin{equation}
f(t)=\frac{4}{\pi}\sum_{n=\text{odd number}}^{\infty}\frac{1}{n}\sin n\omega t\\
=\frac{4}{\pi}\left( \sin \omega t + \frac{1}{3}\sin 3\omega t+\frac{1}{5}\sin 5\omega t +\dots\right)\\
=\frac{4}{\pi} \sin 2\pi f t + \frac{4}{3 \pi}\sin 6\pi f t+\frac{4}{5\pi}\sin 10\pi f t +\dots
\end{equation}
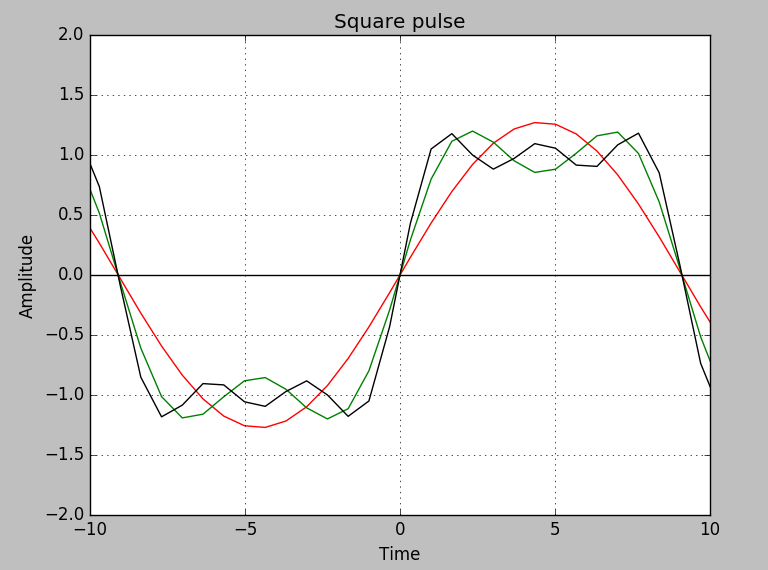
(5)式の第3項までをグラフに描画する. 第1項が赤, 第1項と第2項の和が緑, 第3項までの和が黒の曲線で示されている.
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(8,6), dpi=100)
ax = fig.add_subplot(111)
f = 10000
t = np.linspace(-100, 100, 300, endpoint=True)
ft1 = (4/(np.pi))*(np.sin(2*np.pi*f*t))
ft2 = (4/(np.pi))*(np.sin(2*np.pi*f*t))+(4/(3*np.pi))*(np.sin(3*2*np.pi*f*t))
ft3 = (4/(np.pi))*(np.sin(2*np.pi*f*t))+(4/(3*np.pi))*(np.sin(3*2*np.pi*f*t))+(4/(5*np.pi)*np.sin(5*2*np.pi*f*t))
plt.plot(t,ft1,linewidth=1, color='R')
plt.plot(t,ft2,linewidth=1, color='G')
plt.plot(t,ft3,linewidth=1, color='K')
plt.ylim(-2, 2)
plt.xlim(-10, 10)
plt.axhline(y=0, color='k')
plt.title('Square pulse')
plt.xlabel('Time')
plt.ylabel('Amplitude')
ax.grid(True)
plt.show()
緩やかなサインカーブ(低周波)が方形波の大まかな輪郭を形成し, 高周波が角の尖った部分を形作ることが読み取れる.
偶関数の場合
次に,偶関数の方形波で同様にフーリエ級数展開を行ってみる.
# -*- coding: utf-8 -*-
from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(8,6), dpi=100)
ax = fig.add_subplot(111)
x = np.linspace(-100, 100, 115, endpoint=True)
y = 1 * signal.square(np.pi * (x-11.5))
plt.plot(x, y,linewidth=2, color='k')
plt.ylim(-2, 2)
plt.xlim(-10, 10)
plt.axhline(y=0, color='k')
plt.title('Square pulse')
plt.xlabel('Time')
plt.ylabel('Amplitude')
ax.grid(True)
plt.show()
この方形波は偶関数($f(t)=f(-t)$)であるから, $\sin n\omega x$の項は消え,$\cos n\omega x$の項のみが残る.すなわち, フーリエ係数$a_n$が残る.
$f(t)=\pm 1$として計算する.
フーリエ係数$a_n$は,
\begin{equation}
a_n=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)\cos n\omega t dt \qquad (n=1,2,3 \dots )\\
=\frac{2}{T}\left\lbrace \int_{-\frac{T}{2}}^{-\frac{T}{4}} -\cos n\omega t dt+\int_{-\frac{T}{4}}^{\frac{T}{4}} \cos n\omega t dt + \int_{\frac{T}{4}}^{\frac{T}{2}} -\cos n\omega t dt\right\rbrace\\
=\frac{2}{T}\left\lbrace \left[\frac{-1}{n\omega} \sin n\omega t \right]_{-\frac{T}{2}}^{-\frac{T}{4}} + \left[ \frac{1}{n\omega}\sin n\omega t\right]_{-\frac{T}{4}}^{\frac{T}{4}}+ \left[ \frac{-1}{n\omega}\sin n\omega t\right]_{\frac{T}{4}}^{\frac{T}{2}} \right\rbrace\\
=\frac{2}{n\omega T}\left\lbrace -[\sin \frac{-n\pi}{2}-\sin (-n\pi)]+ [\sin \frac{n\pi}{2}-\sin \frac{-n\pi}{2}]-[\sin n\pi-\sin \frac{n\pi}{2}] \right\rbrace\\
=\frac{2}{n\omega T}\left\lbrace -[-\sin \frac{n\pi}{2}-0]+ [\sin \frac{n\pi}{2}+\sin \frac{n\pi}{2}]-[0-\sin \frac{n\pi}{2}] \right\rbrace\\
=\frac{2}{(2m-1)\pi}\lbrace -2(-1)^m\rbrace.
\end{equation}
ここで,
\[
\sin n \frac{\pi}{2}=-(-1)^n
\]
である.$n$が偶数のとき,$\sin n \frac{\pi}{2}=0$より,
\[
n=2m-1 \qquad (n=1,3,5 \dots)
\]
と置き換えた.
ゆえに,
\begin{equation}
b_n = \left\lbrace
\begin{array}{cc}
\frac{4}{(2m-1)\pi} \qquad\text{m=1,5,9,...}\\
-\frac{4}{(2m-1)\pi}\qquad\text{m=3,7,11,...}
\end{array}
\right\rbrace
\end{equation}
これより,
\begin{equation}
f(t)=\frac{4}{\pi}\sum_{m=1}^{\infty}\frac{-(-1)^m}{2m-1}\cos (2m-1)\omega t\\
=\frac{4}{\pi}\left( \cos \omega t - \frac{1}{3}\cos 3\omega t+\frac{1}{5}\cos 5\omega t- \dots\right)\\
=\frac{4}{\pi} \sin 2\pi f t - \frac{4}{3 \pi}\cos 6\pi f t+\frac{4}{5\pi}\cos 10\pi f t- \dots
\end{equation}
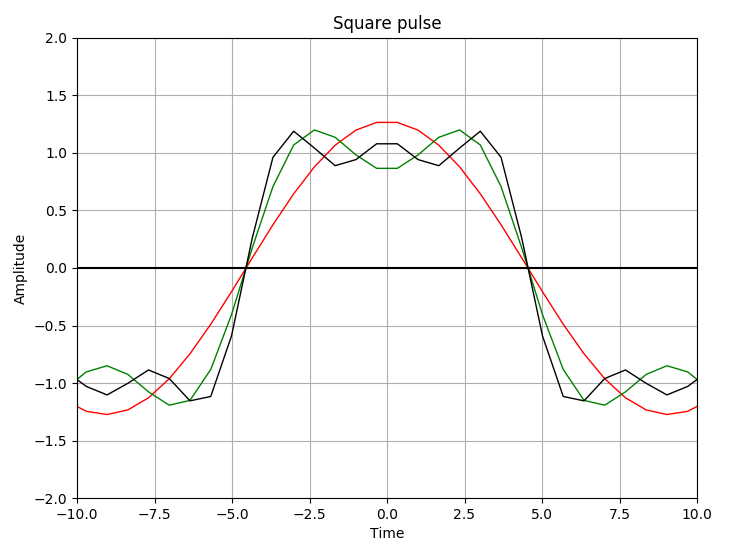
(8)式の第3項までをグラフに描画する. 第1項が赤, 第1項と第2項の和が緑, 第3項までの和が黒の曲線で示されている.
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(figsize=(8,6), dpi=100)
ax = fig.add_subplot(111)
f = 10000
t = np.linspace(-100, 100, 300, endpoint=True)
ft1 = (4/(np.pi))*(-np.cos(2*np.pi*f*t))
ft2 = (4/(np.pi))*(-np.cos(2*np.pi*f*t))+(4/(3*np.pi))*(np.cos(3*2*np.pi*f*t))
ft3 = (4/(np.pi))*(-np.cos(2*np.pi*f*t))+(4/(3*np.pi))*(np.cos(3*2*np.pi*f*t))-(4/(5*np.pi)*np.cos(5*2*np.pi*f*t))
plt.plot(t,ft1,linewidth=1, color='R')
plt.plot(t,ft2,linewidth=1, color='G')
plt.plot(t,ft3,linewidth=1, color='K')
plt.ylim(-2, 2)
plt.xlim(-10, 10)
plt.axhline(y=0, color='k')
plt.title('Square pulse')
plt.xlabel('Time')
plt.ylabel('Amplitude')
ax.grid(True)
plt.show()
偶関数でも奇関数と同様に, 低周波が方形波の大まかな輪郭を形成し, 高周波が角の尖った部分を形作ることが読み取れる.
[注記]2019.12.13
なお,上述のサイン波・コサイン波の周期はグラフの横軸を見ると, 約18秒. すなわち, 周波数はおよそ$1/18=0.056$Hzである.
pythonコードでは, "$f=10000$"とパラメータを置いているが, プロットする点の数などによって変動するので暫定値としている.
今後の宿題
擬似的に,だがアナログ発振回路でも方形波(脈動)を作ることができる.
[>>>(バイポーラ)トランジスタ 2SC1815L-Yを用いたアナログ発振回路]
この中で,回路図と
そのシミュレーション結果に基づく電圧値(3カ所)を示したグラフをみると,
非安定マルチバイブレータからディレイ回路に信号が入るV(006)が擬似的な方形波になっている.発光ダイオード(LED)からトランジスタのコレクタへ出力された信号はノコギリ波のように見える.
今回, フーリエ級数展開したことで, 方形波を特徴付ける要素としての波形が抽出された.それでは, それらの要素となる波形を(抵抗,コイル,コンデンサという)アナログ素子をうまく組み合わせて作ることができたならば, 様々な方形波を自由に生成できるのではないだろうか.さらに,要素となる波形を増やすことで, 回路シミュレーションで擬似的に生成される方形波の凹凸形状の精度を,より鋭いものに高められるのではないだろうか. ひとまず,これらは宿題として取っておこう.
index.htmlに戻る



