物理のノート
公式類>ベクトル解析>テンソル
テンソル
3次元ベクトル空間$V^3$では, 内積$\pmb a \cdot \pmb b$と外積$\pmb a \times \pmb b$を定義することができる.
これらの定義を任意次元のベクトル空間$V^n$に拡張する.
内積は3次元ベクトルのように捉えることができる. 一方、外積は, 3次元ベクトルのように立体的に考えることはできない（できる人もいる？）が, 計算上では$V$の基底$\pmb e_1, \dots, \pmb e_n$を変数とする多項式が得られる.
これを$V$上のテンソル代数, また, その元（げん）をテンソルと呼ぶ.
2つのベクトル空間$V$, $W$の積を, 新たなベクトル空間$V \otimes W$と定義する.
ベクトル空間$V \otimes W$は, ベクトル空間$V$, $W$のテンソル積という.
一般にベクトル$\pmb a$, $\pmb b$の外積$\pmb a \wedge \pmb b$はテンソル積を用いて次のように表す.
\[
\pmb a \wedge \pmb b=\pmb a \otimes \pmb b - \pmb b \otimes \pmb a
\]
さて,
\begin{equation}
V=(V^*)^*
\end{equation}
となるようなベクトル空間$V^*$を, $V$の双対ベクトル空間（または双対空間）と呼ぶ.
$V$の基底を$\pmb e_i$とするとき, $V^*$の基底$\pmb e_j^*$で内積をとる.
\begin{equation}
\pmb e_i \pmb e_j^*=\delta_{ij}
\end{equation}
$\delta_{ij}$:クロネッカーのデルタ（>>> 複素フーリエ係数
$c_n$を求める際の考え方）
\[
\delta_{ij}=\binom{0}{1}
\]
ただし, $i \ne j$の時, $\delta_{ij}=0$（直交関係である,といっても立体空間における"直角"の位置関係を表すわけではない. あくまで計算上の話である.）,
$i = j$の時, $\delta_{ij}=1$
の関係がある. 基底$\pmb e_j^*$を$\pmb e_i$の双対基底という.
ベクトル空間$V$において、$\pmb R$（実数の集合：実数体）,$V$,$V^*$からいくつかのテンソル積を作って得られる空間, 例えば
\begin{equation}
V \otimes V \otimes V \otimes V^* \otimes V \otimes V^*
\end{equation}
の元も, 前述の定義の通り, テンソルと呼び, $\pmb C$などで表す.
＊ テンソル積で得られた空間は, 群論（群の定義）では生成元の積（または連接）で作られた自由群といえる.
さてテンソルを型に分ける. $V$を$1$, $V^*$を$-1$とすると,(3)の場合は,$ [1,1,1,-1,1,-1]$型と表現する.
ただし、
\[
V \otimes V^*=V^* \otimes V
\]
同型であることから,(3)式の$V$,$V^*$を入れ替えてまとめる.
\begin{equation}
V \otimes V \otimes V \otimes V\otimes V^* \otimes V^*
\end{equation}
＊ 同型に関する定理によると, 領域$D$の$O$を起点とする基本群（Fundamental group, 1-homotopy group, または, ポアンカレ群）$\pi_1(D;O)$について,$D$に含まれる$O^{'}$
を起点とする$\pi_1(D;O^{'})$と, $\pi_1(D;O)$は同型である, という（参考文献「ガロアの夢」）.
＊ なお, 線形写像であると同時に, 積も保つ写像として拡張できる場合は, 準同型写像という.
さて, 上記同型の場合, $V$,$V^*$の数はそれぞれ$4$,$2$であることから, $(4,2)$型である,という.
一般化するとベクトル空間$V$上の$(p,q)$型のテンソル全体を$\pmb T_q^p(V)$と記すことにする.
そして,
\[
\pmb T_0^0(V)=\pmb R
\]
の元をスカラー,
\[
\pmb T_0^1(V)=V
\]
の元を反変ベクトル,
\[
\pmb T_1^0(V)=V^*
\]
の元を共変ベクトルと呼ぶ.
また, $\pmb T_q^p(V)$または$(p,q)$型のテンソルをp階反変q階共変テンソル,$\pmb T_0^p(V)$または$(p,0)$型のテンソルをp階反変テンソル,
$\pmb T_q^0(V)$または$(0,q)$型のテンソルをq階共変テンソルと称する.
したがって, 1階反変テンソルの元は反変ベクトル, 1階共変テンソルの元は共変ベクトルとなる.
$p \ne 0$, かつ $q \ne 0$の場合は,$(p,q)$型テンソルを混合テンソルと呼ぶ.
ベクトルと多様体
多様体とは, 曲面を高次元に一般化した"曲がった空間"のことを示す.
しかし, 多様体は局所的には「ユークリッド空間$E^n$（それを抽象化したアフィン空間$A^n$）と同じ構造を持つ空間」, すなわち「アフィン空間の部分領域」である.
ただし, 議論においては, 我々はこの「アフィン空間の部分」の外部については, 一切知らない（関係を持つことができない）として進められる.
多様体は曲がった空間なので, 曲線座標しか用いることができない.
したがって多様体の上で定義された微分形式である, 反対称共変テンソル場や反変ベクトル場で考察を行う.
微分幾何は, 多様体を微積分の方法を使って調べる学問であり, 現代的な意味での微分幾何はGaussが1827年に発表した曲面の研究に始まる.
一般にアフィン空間$A^n$で定義されたテンソル場$\pmb T(\pmb x)=(T_{ij}(\pmb x))$などについては, 各点$x$における演算の他に, 独立変数に関する微分が認められる.
\[
\pmb T(\pmb x)=(T_{j_1 \dots j_q}^{i_1 \dots i_p}(\pmb x))
\]
が$(p,q)$型テンソル場であるとき, 次の偏導関数
\[
\nabla_j T_{j_1 \dots j_q}^{i_1 \dots i_p} (x)=\frac{\partial T_{j_1 \dots j_q}^{i_1 \dots i_p}}{\partial x^j}
\]
を成分とする
\[
\nabla \pmb T (x)=(\nabla_j T_{j_1 \dots j_q}^{i_1 \dots i_p}( x))
\]
は, $(p,q+1)$型テンソル場となる.
3次元のベクトル解析に用いる演算は, すべてテンソル場の微分を用いて表すことができる.
縮約はスカラー場であり, この勾配$\text{grad} \pmb T$は共変ベクトルになる.
発散$\text{div} \pmb f$は, $\pmb f$を反変ベクトル場として微分した混合テンソル場$\nabla_j f^i$のトレースである.
回転$\text{rot} \pmb f$は, $\pmb f$を共変ベクトル場として微分した2階共変テンソル場$\nabla_j f_i$の, 反対称部分の2倍, $\nabla_j f_i-\nabla_i f_j$とみなすことができる.
ミンコフスキー空間
符号指数$(1,3)$を持つ2次形式$\pmb G(\pmb x)$を1つ固定した4次元のベクトル空間$M$をミンコフスキー・ベクトル空間といい, 同じもので原点0を固定せずに考えるとき,
ミンコフスキー空間と称する.
ユニタリ・ベクトル空間（複素ユークリッド・ベクトル空間）
正定符号エルミート形式$\pmb G(\pmb x)$を指定した複素ベクトル空間をユニタリ・ベクトル空間（複素ユークリッド・ベクトル空間）と呼ぶ.
ユニタリ・ベクトル空間$V^n$の複素正則線形変換であり, なおかつベクトルの長さを変えない場合をユニタリ変換という.
ユニタリ変換全体$U(V^n)$も群をなし,ユニタリ群と呼ぶ.
基本計量テンソル
一般のベクトル空間$V$上のテンソルは, 型が異なる場合に座標変換に対して異なった振る舞いをする.
しかし, ユークリッド・ベクトル空間やシンプレティック・ベクトル空間など非退化（符号指数$(p,q)$に対して$p+q$は$V$の次元に等しいとの仮定をする）な双線形形式$\pmb G(\pmb x,\pmb y)$（極座標）が1つ指定され,
なおかつこの双線形形式が線形変換において保存されるような, 幾何固有の変換が許される場合には, 型の異なるテンソルも同一視することができる.
基本双線形形式
\begin{equation}
\pmb G(\pmb x,\pmb y)=\sum_{i,j=1}^n g_{ij}x^i y^j
\end{equation}
を, テンソル$V$上における2階対称共変テンソルとみなしたものを, 基本計量テンソルと呼ぶ.
非退化の場合, ベクトル$\pmb y \in V$と, 線形形式$\pmb G(\pmb \cdot, \pmb y) \in V^*$は1対1で対応する.言い換えると, 双線形形式$\pmb G$を介して,
$V$上の反変ベクトルと共変ベクトルは1対1で対応する.これらを同伴ベクトルと呼び, テンソル解析では同一視することが多い.
それぞれの$y^i$成分,$y_i$成分について同じベクトル$\pmb y$の反変成分、共変成分とみなす.
\[
y_i=\sum_{j-1}^n g_{ij}y^j,\\
y^i=\sum_{j-1}^n g^{ij}y_j
\]
形の上では添え字の位置だけことなる. これらをの添え字の上げ,下げという.
3次元ベクトル空間における曲面の第一基本形式
次の式で表される$ds^2$を, 3次元ベクトル空間における曲面の第一基本形式（または,Riemann（リーマン）計量と呼ぶ. 基本計量テンソルと類似している.
[>>>ポアンカレ計量]
\begin{equation}
ds^2=\sum g_{ij}du^i du^j
\end{equation}
$i$,$j$は添え字である.
第二基本形式
曲面上のベクトル$\pmb p$を次のように表すことにする.
\[
\pmb p=\pmb p (u,v)=(x(u,v)),y(u,v),z(u,v))
\]
偏微分を添え字で表して, 次のように書き記す.
\[
\pmb p_{uv}=\frac{\partial^2 \pmb p}{\partial u \partial v}\\
=\left(\frac{\partial^2 x}{\partial u \partial v},\frac{\partial^2 y}{\partial u \partial v},\frac{\partial^2 z}{\partial u \partial v}\right )
\]
$\pmb p_u(u_0,v_0)$,$\pmb p_v(u_0,v_0)$はともに, $\pmb p(u_0,v_0)$における接ベクトルとなる（一次独立で, 接平面の基）.
外積$\pmb p_u \times \pmb p_v$は, 接平面と直交するベクトルであり, 自身の長さ$\lvert \pmb p_u \times \pmb p_v \rvert$で割った$\pmb e$すなわち単位方ベクトルは
次のように記される.
\begin{equation}
\pmb e=\frac{1}{\lvert \pmb p_u \times \pmb p_v \rvert} \pmb p_u \times \pmb p_v
\end{equation}
接ベクトル$\pmb p_u(u_0,v_0)$,$\pmb p_v(u_0,v_0)$と, 単位方ベクトル$\pmb e$は直交する.したがって内積$\cdot$（ドット積）を用いて,
\begin{equation}
\pmb p_u \cdot \pmb e=0
\end{equation}
\begin{equation}
\pmb p_v \cdot \pmb e=0
\end{equation}
（8）式の両辺を$\frac{\partial}{\partial u}$で偏微分する.
\begin{equation}
\frac{\partial}{\partial u} (\pmb p_u \cdot \pmb e)=\frac{\partial}{\partial u}\frac {\partial \pmb p}{\partial u} \cdot \pmb e+\pmb p_u \cdot \frac{\partial}{\partial u}\pmb e\\
=\pmb p_{uu} \cdot \pmb e + \pmb p_u \cdot \pmb e_u=0
\end{equation}
同様に偏微分を実行して,
\[
\pmb p_{uv} \cdot \pmb e + \pmb p_u \cdot \pmb e_v=0,\\
\pmb p_{vu} \cdot \pmb e + \pmb p_v \cdot \pmb e_u=0,\\
\pmb p_{vv} \cdot \pmb e + \pmb p_v \cdot \pmb e_v=0.
\]
これらの結果を用いて, 関数$L,M,N$を次のように定義する.
\[
L=\pmb p_{uu} \cdot \pmb e =- \pmb p_u \cdot \pmb e_u,\\
M=\pmb p_{uv} \cdot \pmb e =- \pmb p_u \cdot \pmb e_v\\
=\pmb p_{vu} \cdot \pmb e =-\pmb p_v \cdot \pmb e_u,\\
N=\pmb p_{vv} \cdot \pmb e =-\pmb p_v \cdot \pmb e_v.
\]
ここで次のように, 内積$\cdot$（ドット積）, 関数$L,M,N$を用いて表す式を, 第二基本形式と定義する.
\begin{equation}
-d\pmb p \cdot d\pmb e=Ldu^2+2M du dv + N dv^2
\end{equation}
これに対して 第一基本形式は,内積$\cdot$（ドット積）, 関数$E,F,G$を用いて次のように表される.
\begin{equation}
d\pmb p \cdot d\pmb p=Edu^2+2F du dv + G dv^2
\end{equation}
Gauss曲率
第一基本形式と第二基本形式に含まれる関数を用いて,Gauss曲率$K$を次のように定義する.
\begin{equation}
K=\frac{LN-M^2}{EG-F^2}
\end{equation}
曲線の長さ
第一基本形式またはリーマン計量$ds^2=\sum g_{ij}du^i du^j$により,曲線$\gamma(t)=(u^1(t),u^2(t)), 0\leqq t\leqq a$の長さ$L(\gamma)$は,
\begin{equation}
L(\gamma)=\int_0^a \sqrt {\sum g_{ij} \frac{du^i}{dt}\frac{du^j}{dt}}dt
\end{equation}
と記される.
この曲線$\gamma(t)$が二点$p=\gamma(0),q=\gamma(1)$を結ぶ最短距離であるための条件は, すべての$\varepsilon$に対して,
\[
L(\gamma_\varepsilon)\geqq L(\gamma).
\]
ここで曲線$\gamma_\varepsilon$とは,点$p,q$を固定して曲線$\gamma$を少し動かして得られる曲線を指すものとする.
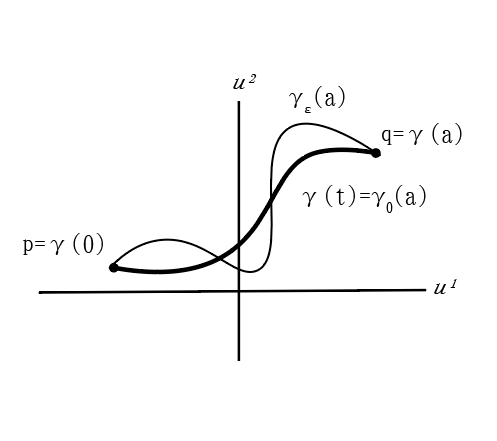すなわち
\begin{equation}
\gamma_\varepsilon(t)=(u^1(t)+\varepsilon\xi^1(t),u^2(t)+\varepsilon\xi^2(t)),\\
0\leqq t \leqq a, \lvert\delta\rvert=\varepsilon
\end{equation}
を満たすような,曲線の族を考える.
ここで,
\begin{equation}
\gamma_0=\gamma, \xi^i(0)=\xi^j(a)=0
\end{equation}
とする.したがって,
\[
\gamma_\varepsilon(0)=\gamma(0),\\
\gamma_\varepsilon(a)=\gamma(a).
\]
曲線の長さ$L(\gamma_\varepsilon)$を$\varepsilon$の関数とすると, $\varepsilon=0$（二つの曲線$\gamma_\varepsilon$と$\gamma$が一致）で最小値をとるためには,次式を満たす必要がある.
\begin{equation}
\frac{d}{d\varepsilon} L(\gamma_\varepsilon)\vert_{\varepsilon=0} =0.
\end{equation}
(14)(15)式より,
\begin{equation}
L(\gamma_\varepsilon)=\int_0^a \sqrt {\sum g_{ij}(\gamma_\varepsilon(t)) \frac{d(u^i(t)+\varepsilon\xi^i(t))}{dt}\frac{d(u^j(t)+\varepsilon\xi^j(t))}{dt}}dt
\end{equation}
を得て, $\varepsilon$で微分して,$\varepsilon=0$とおく.すなわち(17)式より
\begin{equation}
\frac{d}{d\varepsilon} L(\gamma_\varepsilon)\vert_{\varepsilon=0} =\int_0^a \sum \left(\frac{\partial g_{ij}}{\partial u^k} \xi^k \frac{du^i}{dt}\frac{du^j}{dt}+2g_{ij}\frac{d\xi^i}{dt}\frac{du^j}{dt}\right)dt
\end{equation}
となる.
ここで,次の部分積分を行う.
\begin{equation}
\frac{d}{dt}\sum g_{ij}\xi^i\frac{du^j}{dt}=\sum \left(\frac{\partial g_{ij}}{\partial u^k}\frac{du^k}{dt}\xi^i \frac{du^j}{dt}+g_{ij}\frac{d\xi^i}{dt}\frac{du^j}{dt}+g_{ij}\xi^i\frac{d^2 u^j}{dt^2}\right).
\end{equation}
この部分積分の結果と,(7)式すなわち$\gamma_0=\gamma, \xi^i(0)=\xi^j(a)=0$を適用すると(19)式は,
\begin{equation}
\frac{d}{d\varepsilon} L(\gamma_\varepsilon)\vert_{\varepsilon=0} =-2\int_a^b \sum \left\lbrace g_{kj}\frac{d^2 u^j}{dt^2}+\left(\frac{\partial g_{kj}}{\partial u^i}-\frac{1}{2}\frac{\partial g_{ij}}{\partial u^k}\right)\frac{du^i}{dt}\frac{du^j}{dt}\right\rbrace \xi^k dt
\end{equation}
となる.
(21)式の右辺が0になるには,
\begin{equation}
\sum_{i,j} g_{kj}\frac{d^2 u^j}{dt^2}+\left(\frac{\partial g_{kj}}{\partial u^i}-\frac{1}{2}\frac{\partial g_{ij}}{\partial u^k}\right)\frac{du^i}{dt}\frac{du^j}{dt}=0\\
(k=1,2)
\end{equation}
が成立する必要がある.(22)式を測地線の微分方程式と呼ぶ.この方程式を満たすような曲線を測地線と称する.
index.htmlに戻る