物理のノート
電磁気回路の基礎と応用>LRC回路
スミスチャートと双曲幾何
双曲幾何
ユークリッドの公準1から4までを満たし, 公準5を満たさない幾何は双曲幾何に限られる.
ユークリッドの5つの公準は, 次のように記される.
- 1. 与えられた二点$A$,$B$に対し, $A$,$B$を結ぶ線分を1つ, そして唯一引くことができる.
- 2. 与えられた線分は どちら側にも限りなく伸ばすことができる.
- 3. 平面上に二点$A$,$B$が与えられたとき, $A$を中心として$B$を通る円をただ一つ描くことができる.
- 4. 直角はすべて相等しい.
- 5. 二直線と交わる一つの直線が同じ側につくる内角の和が二直角より小さいならば, 二直線をその側に伸ばせばどこかで交わる.
参考："EUCLID’S ELEMENTS OF GEOMETRY" > "Book1 Fundamentals of Plane Geometry Involving
Straight-Lines" > P.7 "Postulates"
複比
$z_1$,$z_2$,$z_3$,$z_4$を複素数（実数でもよい）とする.
\begin{equation}
[z_1,z_2,z_3,z_4]=\frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)}
\end{equation}
これを, $z_1$,$z_2$,$z_3$,$z_4$を
複比（
非調和比：cross ratio）と呼ぶ.
ここで, $z_1$,$z_2$,$z_3$を相違なる数として固定する. $z_4$を変数と見なして$z$として, 複比$ [z_1,z_2,z_3,z_4]$を$z$の関数と考え
$\lambda(z)$とする.
\begin{equation}
\lambda(z)=\frac{(z_1-z_3)(z_2-z)}{(z_2-z_3)(z_1-z)}\\
=\frac{-(z_1-z_3)z+z_2(z_1-z_3)}{-(z_2-z_3)z+z_1(z_2-z_3)}\\
=\frac{(z_3-z_1)z+z_2(z_1-z_3)}{(z_3-z_2)z+z_1(z_2-z_3)}
\end{equation}
ここで,
\[
\lambda(z_1)=\frac{(z_1-z_3)(z_2-z_1)}{(z_2-z_3)(z_1-z_1)}=\frac{(z_1-z_3)(z_2-z_1)}{0}=\infty
\]
\[
\lambda(z_2)=\frac{(z_1-z_3)(z_2-z_2)}{(z_2-z_3)(z_1-z_2)}=\frac{0}{(z_2-z_3)(z_1-z_2)}=0
\]
\[
\lambda(z_3)=\frac{(z_1-z_3)(z_2-z_3)}{(z_2-z_3)(z_1-z_3)}=1
\]
すなわち, $z_1$,$z_2$,$z_3$をそれぞれ$\infty$,$0$,$1$に移すような
一次変換により,$z_4$は$ [z_1,z_2,z_3,z_4]$に移る.
[>>>
三相交流電源におけるベクトルオペレータと位相>１次変換]
(2)式に$z_1=\infty,z_2=0,z_3=1,z_4=\lambda$を代入する.
\begin{equation}
\lambda(z)=\frac{(\infty-1)(0-\lambda)}{(0-1)(\infty-\lambda)}=\frac{(\infty-1)\lambda}{\infty-\lambda}\\
=\frac{\frac{\lambda}{\infty}-\lambda}{\frac{\lambda}{\infty}-1}=\lambda
\end{equation}
すなわち,
\begin{equation}
\lambda= [\infty,0,1,\lambda]
\end{equation}
ポアンカレの上半平面モデルと円板モデル
ポアンカレのモデルでは,平面は, 複素平面$\pmb C$の上半平面$\pmb H^+=\lbrace z=x+iy\in \pmb C; y>0\rbrace$として考える.
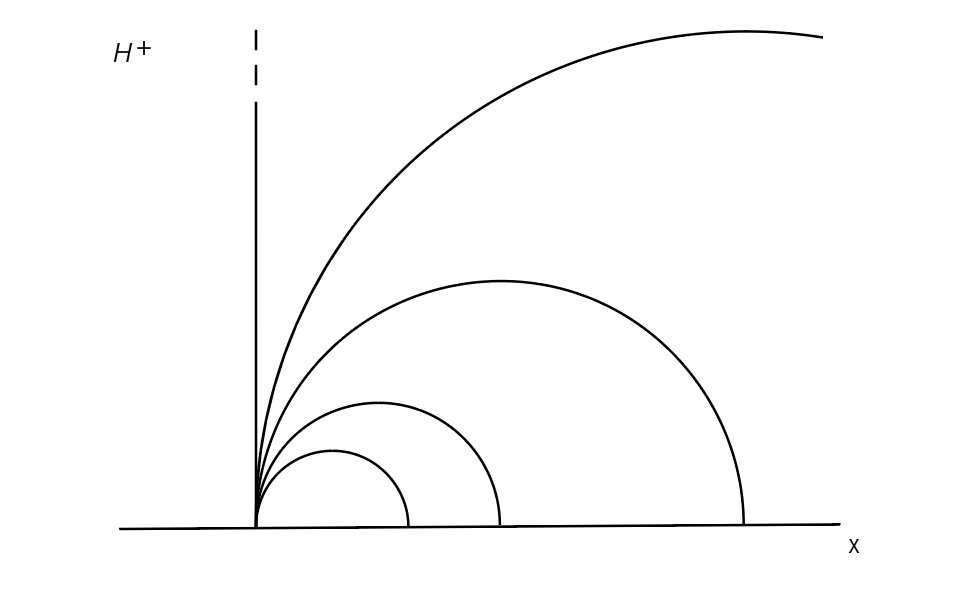
点は, 上半平面$\pmb H^+$（通常の平面（$x,y$）では$y>0$）の範囲内の点を考える.
直線は,$x$軸上に中心を持つ半円を考える. 半径$\infty$の半円は,$x$軸に直交する"半直線"で表される.
上半平面$\pmb H^+$内の線分の長さを定義するために, 複比を用いる.
直線$l$上の二点$z,z^{'}$の長さは, 複比$[z, z^{'}, x_0, x_1]$を用いて,
\[
d(z, z^{'})=\lvert log[z, z^{'}, x_0, x_1] \rvert
\]
と定義する.
\[
d(z, z^{'})=d(z^{'}, z)
\]
である.
上半平面$\pmb H^+=\lbrace z=x+iy\in \pmb C; y>0\rbrace$と単位円$D=\lbrace w=u+iv\in \pmb C; \lvert \omega \rvert ^2=u^2+v^2<1 \rbrace$
は
\begin{equation}
\omega =\frac{i-z}{i+z},z=\frac{i(1-w)}{1+w}
\end{equation}
により, 一対一に対応付けられる.
上半平面を「ポアンカレの上半平面モデル」, 単位円を「ポアンカレの円板モデル」と呼ぶことにする.
$z=x$ならば,
\[
\lvert \omega \rvert=\lvert \frac{i-x}{i+x}\rvert=1.
\]
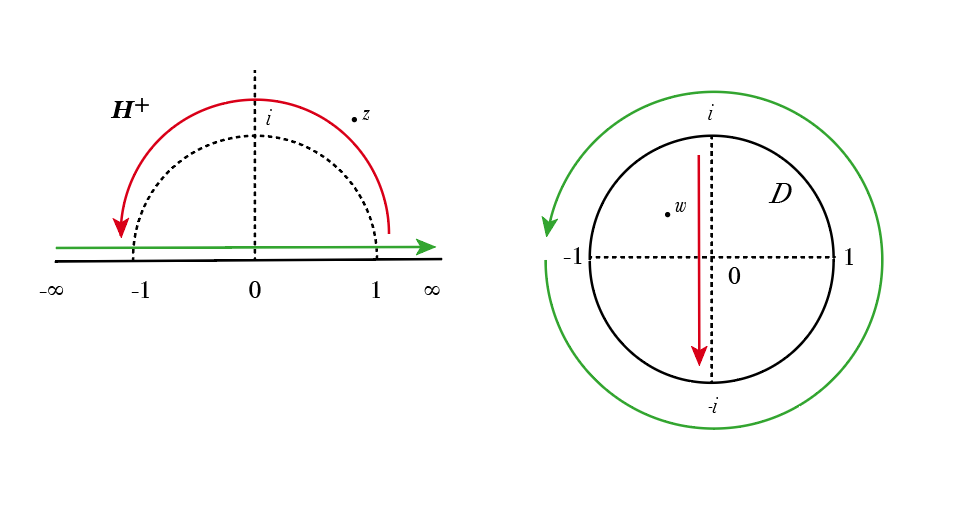
「ポアンカレの上半平面モデル」において, $z=x$が$-\infty, -1, 0, 1 ,\infty$と移動すると,$\omega$が円周上を正の方向に, $-1, -i,1,i,-1$と移動する（緑色の矢印）.
「ポアンカレの上半平面モデル」において,$z$が虚軸上すなわち$z=iy$において$y$が$0,1,\infty$と移動すると,$\omega$は実軸上を負の方向に$1,0,-1$と移動する.
「ポアンカレの円板モデル」において,$z$が半弧上を$1,i,-1$（すなわち$z=e^{it}(=\cos t+ i\sin t)$において$t$が$0,\frac{\pi}{2},\pi$）と移動すると,$\omega$は直径上を$i,0,-i$と移動する（赤色の矢印）.
ポアンカレ計量
上半平面$\pmb H^+=\lbrace z=x+iy\in \pmb C; y>0\rbrace$におけるRiemann（リーマン）計量は次のように記される.
\begin{equation}
ds^2=\frac {dz dz^*}{y^2}=\frac{d(x+iy)d(x-iy)}{y^2}=\frac{dx^2+dy^2}{y^2}
\end{equation}
$z^*(=\bar{z})$は, $z(=x+iy)$の
共役複素数.
このリーマン計量は,
ポアンカレ計量と呼ばれる.[>>>
基本計量テンソル]
上半平面$\pmb H^+$上のポアンカレ計量すなわち
\begin{equation}
ds^2=\frac{dz dz^*}{y^2}
\end{equation}
に対応する, 単位円$D$上の計量を求める.
(1)式$z=\frac{i(1-w)}{1+w}$より,
\begin{equation}
dz=\frac{-2id\omega}{(1+\omega)^2},\\
dz^*=\frac{2id\omega^*}{(1+\omega^*)^2},\\
y=\frac{z-z^*}{2i}=\frac{1-\lvert \omega \rvert ^2}{(1+\omega)(1+\omega^*)}.
\end{equation}
これらを(2)式に代入する.
\begin{equation}
ds^2=\frac{dz dz^*}{y^2}=\frac{\left\lbrace\frac{-2id\omega}{(1+\omega)^2}\right\rbrace \left\lbrace\frac{2id\omega^*}{(1+\omega^*)^2}\right\rbrace}{\left\lbrace\frac{1-\lvert \omega \rvert ^2}{(1+\omega)(1+\omega^*)}\right\rbrace^2}\\
=\frac{4dwdw^*}{(1-\lvert \omega \rvert^2)^2}.
\end{equation}
この結果得られた次式を
\begin{equation}
ds^2=\frac{4dwdw^*}{(1-\lvert \omega \rvert^2)^2}
\end{equation}
単位円版$D=\lbrace \omega\in\pmb C;\lvert\omega\rvert\lt 1\rbrace$のポアンカレ計量と呼ぶ.
index.htmlに戻る
