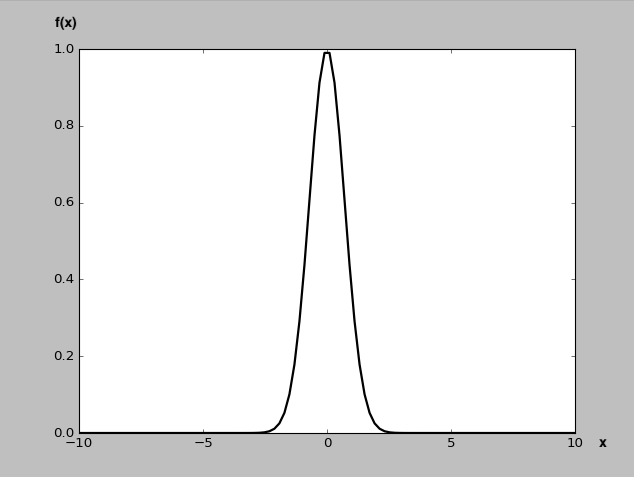
import matplotlib.pyplot as plt
import numpy as np
a = 1
data_x = np.linspace(-10,10,100)
data_y = np.exp( - (a * (data_x **2 )))
plt.plot(data_x,data_y, linewidth=2, color='black')
plt.show()

|
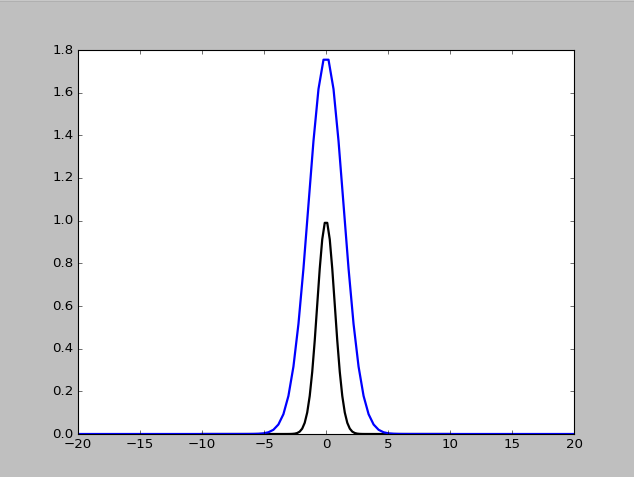 $a=0.1$の場合は次のようになる.
$a=0.1$の場合は次のようになる.
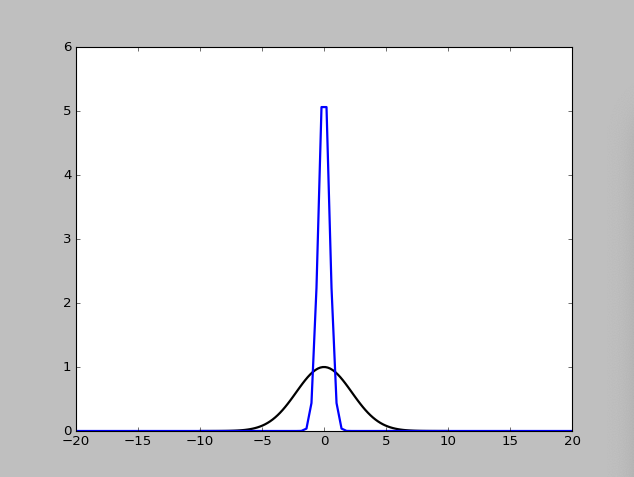 $a=1$,$a=0.1$のグラフをすべて重ねてみると,
$a=1$,$a=0.1$のグラフをすべて重ねてみると,
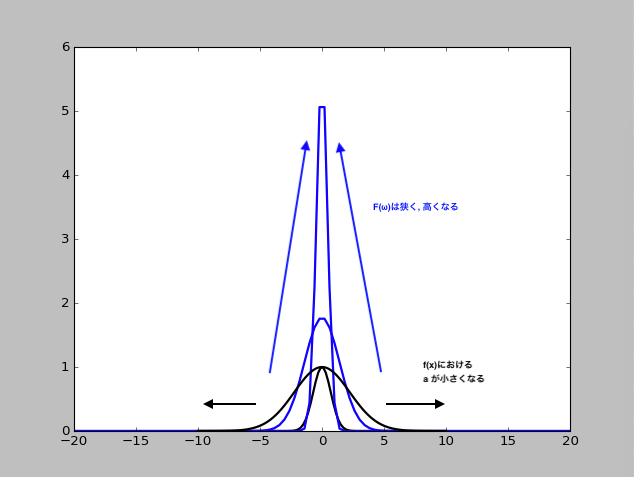 ガウス関数の$a$の値が小さくなる($1\rightarrow 0.1$)ほど(釣鐘の裾が広がるほど), フーリエ変換したガウス関数の幅は狭くなり,高くなる様子がみられる.
このことは, 量子力学における不確定性原理, 例えば座標と運動量にも関係する(という).
index.htmlに戻る
ガウス関数の$a$の値が小さくなる($1\rightarrow 0.1$)ほど(釣鐘の裾が広がるほど), フーリエ変換したガウス関数の幅は狭くなり,高くなる様子がみられる.
このことは, 量子力学における不確定性原理, 例えば座標と運動量にも関係する(という).
index.htmlに戻る